When I was in high school I took a class most students take. It was a trigonometry class. Most of my classmates had a frequent recurring question, “Why do we need to know this?” The teacher wasn’t very helpful with giving an answer. So I took it upon myself to come up with one. Being a youth myself it proved a difficult task. What I came up with were two rather unsatisfying answers. The first answer was simply, “for the test.” My other answer looked a little further into the future and was, “for next year’s class.” Little did I know that I would continue using it for years to come.
Most recently I used trig in programming the camera movement for Windom. There were two rules for it’s motion. One, the camera should move in a parabolic shape vertically, close to the character when low and high and far from the character when in the middle heights. And two, it should move in a circle horizontally around the character. Those of you who know your trig should already see how it will come into play.
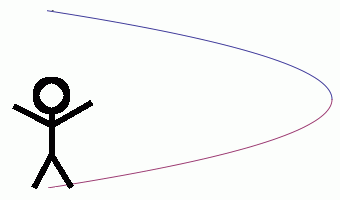
I was working from a drawing of what the motion should be. But what I needed was a function which defines the distance from the character. So as a starting point, I decided to find the function which defines the drawing. Here’s a visual.

Here’s what I knew. The line of symmetry goes through the top of the character, there is a point on the parabola at the character’s feet and one above the character. The function which defines this is h(sqrt(-x/m)+1) where h is the height of the character and m is the furthest distance modifier. It turns out this function isn’t very useful. It gives a height when provided with the distance from the character. I wanted a distance from the character provided with the height. Easy, just take the inverse. The result with some simplification is hm(1-x^2). That is what defines the distance which the camera should be from the character given the height of the camera.
The rest is comparatively easy. I know the rotational point where the camera should be in radians. It is just a matter of using trig to convert to x and z coordinates. I went with x=d*sin(r) and z=d*cos(r) where d is the distance provided by the the function in the previous paragraph and r is the rotational position in radians.
If I didn’t know trig the circular motion part would have been immensely more difficult. When I was in high school I never expected to need trig for very much but now I have more appreciation for it.